集合

算法复杂度分析

❒ 为什么要进行复杂度分析?
✔ 指导你编写出性能更优的代码
✔ 评判别人写的代码的好坏

❒ 大O表示法:不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势T(n)与代码的执行次数成正比(代码行数越多，执行时间越长)
✔ T(n) = O(3n + 3)
✔ T(n) = O(n)
✔ 当n很大时，公式中的低阶，常量，系数三部分并不左右其增长趋势，因此可以忽略，我们只需要记录一个最大的量级就可以了

❒ 描述 表示形式
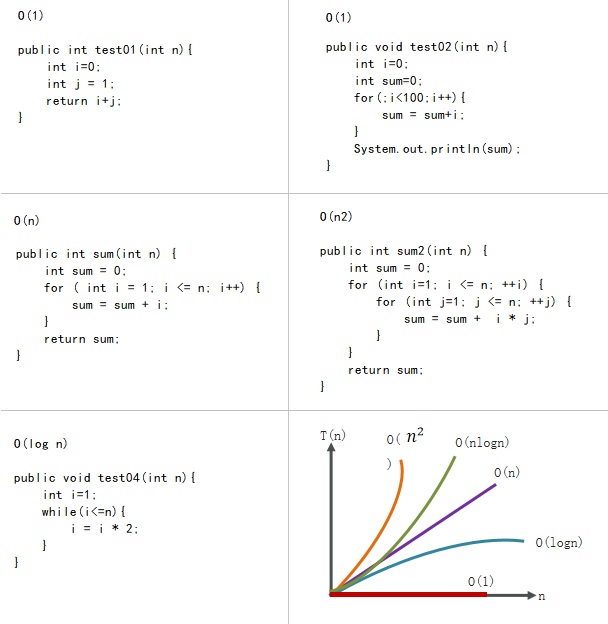
✔ 常数 0(1)：只要代码的执行时间不随着n的增大而增大，这样的代码复杂度都是O(1)
✔ 对数 O(log n)
✔ 线性 O(n)：单重重for循环 O(3n +3)
✔ 线性对数 O(n * log n)：复杂度分析就是要弄清楚代码的执行次数和数据规模n之间的关系
    public void test04(int n){
      int i = 1;
        while(i <= n)
          i = i* 10
    }
✔ 平方 O(n2)：双重for循环 O( 3n²+ 3n +3)
✔ 立方 O(n3)
✔ k次方 O(n* )
✔ 指数 O(2”)
✔ 阶乘 O(n !)

空间复杂度全称是渐进空间复杂度，表示算法占用的额外存储空间与数据规模之间的增长关系
我们常见的空间复杂度就是O(1),0(n),O(n^2)，其他像对数阶的复杂度几乎用不到，因此空间复杂度比时间复杂度分析要简单的多。

❒ 什么是算法时间复杂度?
✔ 时间复杂度表示了算法的执行时间与数据规模之间的增长关系

❒ 常见的时间复杂度有哪些?
✔ 0(1)、0(n)、0(n^2)、o(logn)
✔ 速记口诀:常对幂指阶

❒ 什么是算法的空间复杂度?
✔ 表示算法占用的额外存储空间与数据规模之间的增长关系常见的空间复杂度:O(1)、O(n)、O(n ^2)